Öncelikle bu problemi Python programlama dili ile kodlamaya vesile olan yazıyı (aynı uygulamanın Java programlama dili ile çözümü) ve linkini paylaşmak istiyorum:
Java ile ikinci dereceden denklemin köklerini bulmak
Bu örnekte gerekli ve yeterli teorik anlatım olduğuna göre doğrudan Python ile hem diskriminant hesabı yapan, hem de diskriminant değerine bağlı olarak sistemin reel kökü olup olmadığını kontrol eden, varsa da kaç tane reel kökü olduğunu bulup yazdıran programı hazırlayacağım.
Bu uygulamada kullanacağımız bilgiler:
Python Programlama Dilinde Dört İşlem Matematiksel Örnekler
Python'da Print Fonksiyonu ile Çıktı Almak
Python'da Kullanıcıdan Girdi Almak (input)
Python'da Değişken Kullanımı ve Örnekleri
Python'da sayıların köklerini hesaplama örnekleri
Python'da if (eğer) kullanımı ve örnekleri
Python Kodları:
from math import *
print("ax^2 + bx + c denkleminin varsa köklerini bulmak için;")
a = int(input("a değerini yazın > "))
b = int(input("b değerini yazın > "))
c = int(input("c değerini yazın > "))
delta = b * b - 4 * a * c
if delta<0:
print("sistemin reel kökü yoktur")
elif delta == 0:
kok = (-b - sqrt(delta)) / (2*a)
print("sistemin tek bir reel kökü vardır")
print(kok)
else:
print("sistemin iki farklı reel kökü vardır")
kok1 = (-b - sqrt(delta)) / (2 * a)
kok2 = (-b + sqrt(delta)) / (2 * a)
print(kok1)
print(kok2)
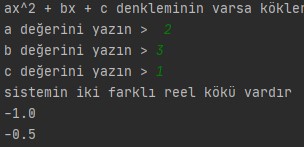
Program Çıktısı: